Kerasではじめての線形回帰
Kerasの環境構築ができたので、さっそく使ってみる。
一番簡単な線形回帰をやってみる。
ライブラリのインポート
使うのは以下。
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, Activation
import numpy as np
標本データの作成
適当に標本データを作ってみる。
\(y = \frac{1}{2} (X_0 + X_1) - 0.5\) とした。
この式が線形回帰によって推測できれば学習成功である。
せっかくだからガウスノイズを加えた。 ちなみにガウス関数は、次のように定義される。
\[f(x) = a \exp{\frac{-(x-b)^2}{2c^2}}\]X = np.random.random((10000, 2))
y_orig = np.mean(X, 1) - 0.5
y_noise = np.random.randn(10000) * 0.1
y = y_orig + y_noise
ノイズをプロットするとこんな感じ。
plt.clf()
plt.plot(np.arange(0, 1000), y_noise[0:1000], '.')
plt.savefig('y_noise.png')
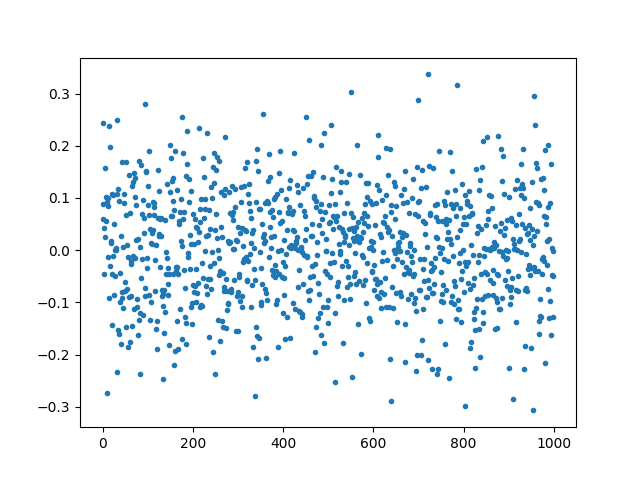
訓練データ, テストデータの作成
訓練データとテストデータ(最終的な成績を測定するデータ)は分けるべきである。 別々に用意するのは面倒なので、さっき作ったデータを分けて使う。
X_train = X[0:9000]
y_train = y[0:9000]
X_test = X[9001:len(X)]
y_test = y[9001:len(y)]
モデル構築
まず、訓練データをプロットしてみる。
fig = plt.figure()
ax3d = mplot3d.Axes3D(fig)
ax3d.scatter3D(X_train[0:1000,0], X_train[0:1000,1], y_train[0:1000])
plt.savefig('Xy_train.png')
次のように、ちょっと厚みのある板みたいな分布になった。
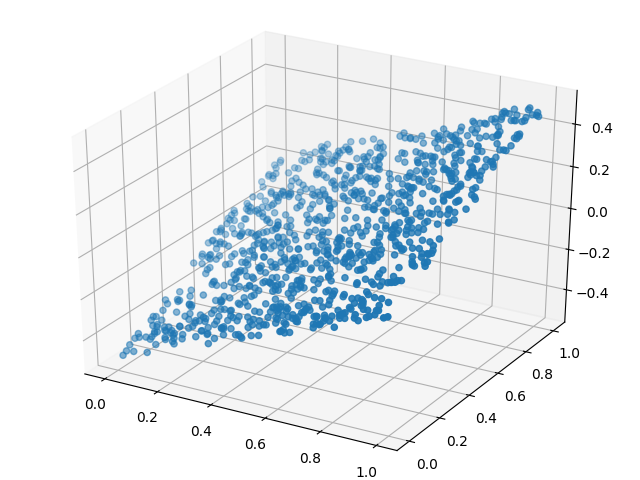
誤差があるけど平面なので一次方程式のように思われる。 というわけで次のようにモデル化する。
\[\begin{align} h(\theta) &= \theta^T X \\ &= \begin{bmatrix} \theta_{00} \theta_{01} \end{bmatrix} \begin{bmatrix} X_0 \\ X_1 \end{bmatrix} + \theta_{10} \\ &= \theta_{00} X_0 + \theta_{01} X_1 + \theta_{10} \end{align}\]\(h(\theta)\) と \(y\) が最も近くなる \(\theta\) を探すのが 機械学習の仕事である。線形回帰ではよく、近さを求めるために二乗誤差を用いる。
この近さを表わす関数を目的関数といい \(J(\theta)\) とかく。 二乗誤差による目的関数は、
\[J(\theta) = \frac{1}{2m} \sum_{i=0}^{m-1}(h_\theta(X) - y)^2\]と表現できる。
Kerasを使うと、この目的関数を最小にするプログラムがすごく簡単に書ける。 簡単すぎて上記目的関数の式を意識する必要すら無い。
それは以下のようなプログラムである。
model = Sequential()
model.add(Dense(1, input_dim=2, kernel_initializer='uniform'))
model.add(Activation('linear'))
model.compile(optimizer='rmsprop', loss='mse')
loss='mse' のところが最小二乗誤差を使え、という意味。
機械学習
実際の学習も簡単に書ける。 次のように書くだけでよい。
hist = model.fit(X_train, y_train, verbose=1)
上の行を実行すると次のように表示される。
9000個のデータについて、10周通して学習をさせている。
回が進むにつれ loss が小さくなり、4周目からあまり変わらなくなっていることから、
4周目で収束していることがわかる。
Epoch 1/10
9000/9000 [==============================] - 0s - loss: 0.0282
Epoch 2/10
9000/9000 [==============================] - 0s - loss: 0.0083
Epoch 3/10
9000/9000 [==============================] - 0s - loss: 5.6706e-04
Epoch 4/10
9000/9000 [==============================] - 0s - loss: 1.0174e-04
Epoch 5/10
9000/9000 [==============================] - 0s - loss: 1.0171e-04
Epoch 6/10
9000/9000 [==============================] - 0s - loss: 1.0116e-04
Epoch 7/10
9000/9000 [==============================] - 0s - loss: 1.0177e-04
Epoch 8/10
9000/9000 [==============================] - 0s - loss: 1.0128e-04
Epoch 9/10
9000/9000 [==============================] - 0s - loss: 1.0190e-04
Epoch 10/10
9000/9000 [==============================] - 0s - loss: 1.0125e-04
テストデータに対する評価をするには evaluate を使う。
>>> scores = model.evaluate(X_test, y_test)
>>> print(scores)
9.53271492153e-05
素晴らしい成績。 学習結果と学習データの誤差がほとんど無い。
学習結果確認
学習した \(\theta\) を取り出す。
>>> theta = model.get_weights()
>>> print(theta[0])
[[ 0.49954879]
[ 0.50138479]]
>>> print(theta[1])
[-0.50062585]
もともとの標本データが \(y = \frac{1}{2} (X_0 + X_1) - 0.5\) だったので、 かなりいい線いっていることがわかった。
自分でも二乗誤差を計算してみる。
さっきの score と似た数字が出た。微妙に違うけどここは深く考えないこととする。
>>> np.sum((y_test - y_pred[0,:]) ** 2)
0.095231809623243222
あとはプロットする。
X_0_mesh = np.linspace(0, 1.0, 11)
X_1_mesh = np.linspace(0, 1.0, 11)
X_0_mesh, X_1_mesh = np.meshgrid(X_0_mesh, X_1_mesh)
y_pred = X_0_mesh * theta[0][0,0] + X_1_mesh * theta[0][1,0] + theta[1][0]
plt.clf()
fig = plt.figure()
ax3d = mplot3d.Axes3D(fig)
ax3d.scatter3D(X_test[:,0], X_test[:,1], y_test[:])
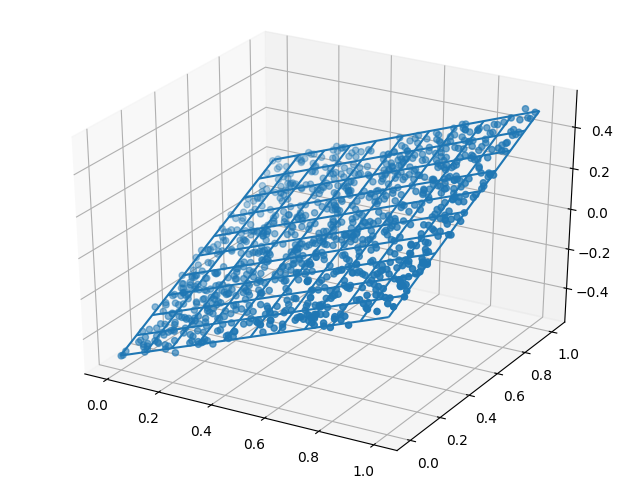
ax3d.plot_wireframe(X_0_mesh, X_1_mesh, y_pred)
plt.savefig('Xy_pred.png')
それっぽい平面を描くことができた。
ソースコード
最後に今回用いたプログラムを貼り付けておく。 ここまでのテキストでは、少しずつ間違いがあるような気もしているが、 以下のプログラムはちゃんと動くはずである。
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers import Dense, Activation
import numpy as np
X = np.random.random((10000, 2))
y_orig = np.mean(X, 1) - 0.5
y_noise = np.random.randn(10000) * 0.1
y = y_orig + y_noise
plt.clf()
plt.plot(np.arange(0, 1000), y_noise[0:1000], '.')
plt.savefig('y_noise.png')
X_train = X[0:9000]
y_train = y[0:9000]
X_test = X[9001:len(X)]
y_test = y[9001:len(y)]
fig = plt.figure()
ax3d = mplot3d.Axes3D(fig)
ax3d.scatter3D(X_train[0:1000,0], X_train[0:1000,1], y_train[0:1000])
plt.savefig('Xy_train.png')
model = Sequential()
model.add(Dense(1, input_dim=2, kernel_initializer='uniform'))
model.add(Activation('linear'))
model.compile(optimizer='rmsprop', loss='mse')
hist = model.fit(X_train, y_train, verbose=1)
scores = model.evaluate(X_test, y_test)
print(scores)
theta = model.get_weights()
X_0_mesh = np.linspace(0, 1.0, 11)
X_1_mesh = np.linspace(0, 1.0, 11)
X_0_mesh, X_1_mesh = np.meshgrid(X_0_mesh, X_1_mesh)
y_pred = X_0_mesh * theta[0][0,0] + X_1_mesh * theta[0][1,0] + theta[1][0]
plt.clf()
fig = plt.figure()
ax3d = mplot3d.Axes3D(fig)
ax3d.scatter3D(X_test[:,0], X_test[:,1], y_test[:])
ax3d.plot_wireframe(X_0_mesh, X_1_mesh, y_pred)
plt.savefig('Xy_pred.png')