KerasではじめてのMLP
今日はMNIST(手書き文字)を、多層パーセプトロン(MLP; Muti Layer Perceptron)を 使って読んでみる。前回までは1層だけのネットワーク?で学習させてきたが、 今回のは入力層と、隠れ層、出力層からなる。
Keras公式のサンプルにあるものと大体同じだが、 Dropout確率の \(p\) を変えて性能を比較してみる。
事前準備
とりあえずKerasライブラリをインポートする。
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
from keras.callbacks import EarlyStopping
次に、学習させるデータを用意する。
今回はMNISTデータセットを使う。 MNISTのロードはKerasの標準ライブラリを使い一撃で可能。すごく親切。
(X_train, y_train), (X_test, y_test) = mnist.load_data()
ロードしたままのデータだと学習に使いにくいため、先に変換する。
\(X_{train}, X_{test}\) の変換。
# 変換前
print('X_train.shape', X_train.shape)
# ('X_train.shape', (60000, 28, 28))
print('X_test.shape', X_test.shape)
# ('X_test.shape', (10000, 28, 28))
# 28x28行列を784ベクタに変換
# Feature 784個としてニューラルネットワークに入力する
X_train = X_train.reshape(60000, 784) # 28 * 28
X_test = X_test.reshape(10000, 784)
# 値域の変換 [0-255] -> [0.0-1.0]
X_train = X_train.astype('float32') / 255
X_test = X_test.astype('float32') / 255
# 変換後
print('X_train.shape', X_train.shape)
# ('X_train.shape', (60000, 784))
print('X_test.shape', X_test.shape)
# ('X_test.shape', (10000, 784))
次に、\(y_{train}, y_{test}\) の変換。
# 変換前
print('y_train.shape', y_train.shape)
# ('y_train.shape', (60000,))
print('y_test.shape', y_test.shape)
# ('y_test.shape', (10000,))
# 正解の数字の列だけ $$ 1 $$、それ以外 $$ 0 $$ のマトリックスに変換
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)
# 変換後
print('y_train.shape', y_train.shape)
# ('y_train.shape', (60000, 10))
print('y_test.shape', y_test.shape)
# ('y_test.shape', (10000, 10))
ミソは to_categorical の変換で、各数字が要素数10のベクトルに変換される。
このベクトルの要素 \(y_k\) は、入力された数字が0〜10である確率 \(p_1, p_2, ..., P_10\) を表わす。
教師データの \(y\) では1要素だけを1、それ以外の要素を0にする。
たとえば、入力の数字が 4 ならば、 y = [ 0 0 0 0 1 0 0 0 0 0 ] とする。
このようにして入力を \(k\) 個のクラスに分類する問題を多クラス問題という。 今回、数字は 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 の10個あるので、10クラスの分類問題ということになる。
また、各クラスを \(C_1, ..., C_k\) と表すとき、\(y_k\) は条件付き確率を使い、 \(p(C_k|X) = y_k\) とも書く。
ソフトマックス関数
このあとも使うが、ソフトマックス関数と呼ばれる関数があり、 ニューラルネットワークで多クラス分類をする場合に一番最後の層の活性化関数として よく使う。
この関数を使った出力を下記のように書く。
\[y_k = z_k^{(L)} = \frac{\exp(u_k^{(L)})}{\sum_{j=1}^{K} \exp(u_j^{(L)})}\]で、この関数は何なのかというと、確率を表現するために都合がいいらしい。 物理的な理由があるわけでは無さそう。
確率表現のために都合がいいという性質は次の通り、とのこと。
(i) \(0 < y_i < 1\) (ii) \(y_1 + y_2 + ... + y_n = 1\) (iii) \(u_j^{(L)}\) のうち、一要素 \(u_n^{(L)}\) だけ他と比べてずっと大きい場合に、\(y_n\) がほぼ \(1\)、それ以外 \(y_m (m \ne n)\) がほぼ \(0\) になる。
なおPythonで実装するには少し工夫が必要である。 上記の通りに実装すると、\(u_j^{(L)}\) が大きい場合に \(\exp(u_j^{(L)})\) が大きくなりすぎて、値がオーバフローしてしまう。
そこで、\(m = \max_i Xi\) としたとき、
\[\begin{align} \sum_i \exp(X_i) &= \sum_i \frac{\exp(m)}{\exp(m)}\exp(X_i) \\ &= \exp(m) \sum_i \frac{\exp(X_i)}{\exp(m)} \\ &= \exp(m) \sum_i \exp(X_i - m) \end{align}\]となることから、
\begin{align}
y_k
&= \frac{\exp(u_k^{(L)})}{\sum_{j=1}^{K} \exp(u_j^{(L)})}
&= \frac{\exp(u_k^{(L)})}{\exp(m) \sum_{j=1}^{K} \exp(u_j^{(L)} - m)}
&= \frac{\exp(u_k^{(L)} - m)}{\sum_{j=1}^{K} \exp(u_j^{(L)} - m)}
\end{align}
と変形できる。
これをプログラムすると、
def softmax(x):
max_x = np.max(x, 1)
exp_x = np.exp(x - max_x[:, None])
return exp_x / np.sum(exp_x, 1)[:, None]
モデル構築
多層パーセプトロンということで、三層のネットワークにする。
1層目は入力層で、入力画像の画素数 784 だけユニットがある。
2層目は隠れ層で512 個のユニット。 なぜ 512 という数字なのかは不明。
最後の出力層は 0〜9 の数字のためのユニットがあるのでユニット 10 個。 出力層の活性化関数に先ほどのソフトマックス関数を使う。
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dense(512, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
categorical_crossentropy は多クラス分類用の交差エントロピーである。
今回は省略する。
学習する
以下プログラムのようにして学習する。
early_stopping = EarlyStopping(monitor='val_loss', patience=2)
hist = model.fit(X_train, y_train, batch_size=128, epochs=20,
validation_split=0.1, verbose=1, callbacks=[early_stopping])
今回も早期打ち切りを有効にしておいた。
学習したあと、学習曲線をプロットしてみる。
plt.clf()
plt.xlabel('epochs')
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['loss'], label='loss')
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['val_loss'], label='val_loss')
plt.legend()
plt.savefig('loss.png')
結果は以下。
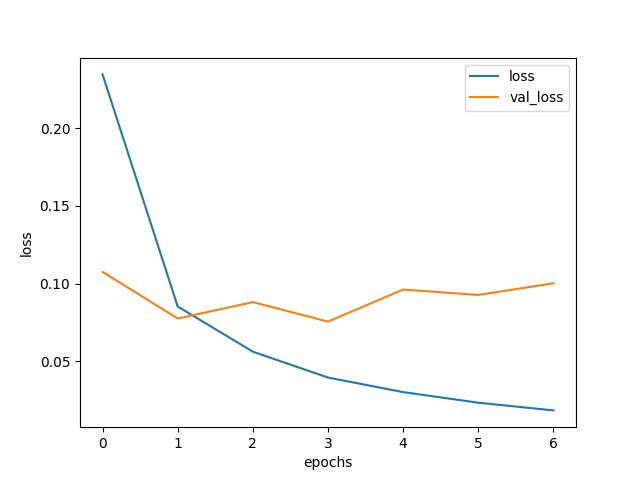
1周目にしていきなり val_loss が増大している。
これはちゃんと学習できる前に過学習が始まっていることを示す。
汎化に失敗しているとも言う。
テストセットを使った評価は次のようにする。
score = model.evaluate(X_test, y_test, verbose=0)
print('score', score)
# ('score', [0.082287257276931036, 0.98250000000000004])
精度98%。たったこれだけでも98点とれるなら、なかなか素晴らしいんじゃないかと思う。 でも100桁読ませたら2桁間違える、と考えるといまいちなのかもしれない。
ドロップアウト
ドロップアウトはネットワーク上の一部ユニットを無効化し、 その状態で学習させるテクニック。 学習時に、各層の各ユニットを確率 \(p\) で無効化する。 Hinton先生らが提案したもので、実装も計算も簡単、汎用性が高く、 かつ過学習の防止に効果的という素敵なテクニックである。
複数種類のネットワークを用意して独立に学習させそれらの平均を取ると 学習精度が上がるというテクニック(モデル平均)もあるらしいが、 ドロップアウトはそれと同じ効果が得られるとのこと。
Kerasでは、Dropout のレイヤーをモデルに追加して上げるだけで、
この恩恵を授かることができる。
以下では、ドロップアウトでユニットを無効化させる確率 \(p\) を 0.1〜0.9 まで変化させ、それぞれで学習する実験をしてみた。
hists = [ hist ]
for p in np.arange(0.1, 0.9, 0.1):
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(p))
model.add(Dense(512, activation='relu'))
model.add(Dropout(p))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
early_stopping = EarlyStopping(monitor='val_loss', patience=2)
hist = model.fit(X_train, y_train, batch_size=128, epochs=20,
validation_split=0.1, verbose=1, callbacks=[early_stopping])
hists.append(hist)
score = model.evaluate(X_test, y_test, verbose=0)
print('score', score)
そして学習データセットに対する精度とバリデーションセットに対する精度を プロットしてみた。
plt.clf()
plt.xlabel('epochs')
plt.ylabel('loss')
for i in range(0, len(hists)):
hist = hists[i]
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['loss'], label='$ p={} $'.format(i * 0.1))
plt.legend()
plt.savefig('train_loss_dropout.png')
plt.clf()
plt.xlabel('epochs')
plt.ylabel('validation loss')
for i in range(0, len(hists)):
hist = hists[i]
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['val_loss'], label='$ p={} $'.format(i * 0.1))
plt.legend()
plt.savefig('val_loss_dropout.png')
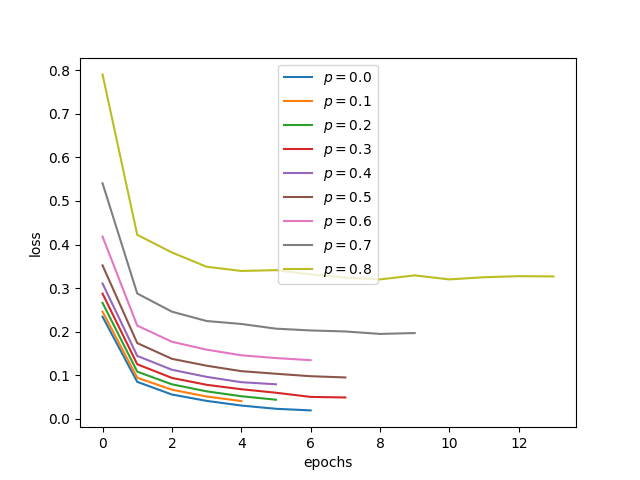
学習データセットに対す学習曲線
\(p\) が大きくなるほど、損失が大きくなっていることがわかる。 ドロップアウトが少ないほど、学習データへピッタリ合わせられる、 というのは直感に反していない。
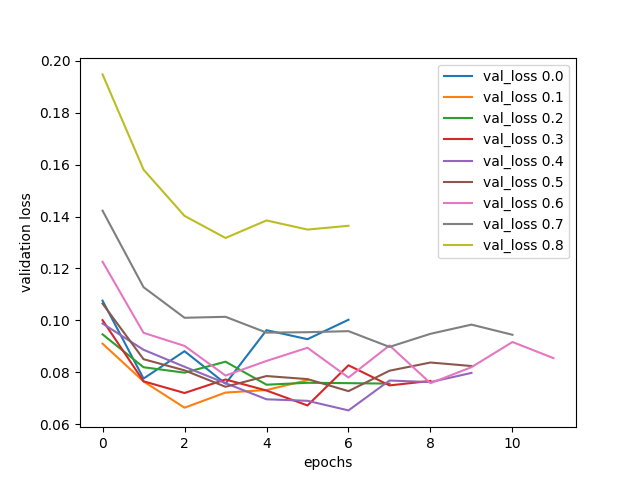
バリデーションセットに対する学習曲線
\(p\) が大きいほど、バリデーションセットの損失の増加し始めが遅れている。
ドロップアウト無し(\(p = 0\))、または\(p = 0.1\) のとき、 1周目、2周目で過学習してしまっている。
\(p = 0.2-0.6\) だと、それなりにまともな学習できていそうに見える。 いずれも \(損失 < 0.7)\) 程度である。
\(p \ge 0.7\) だと過学習が始まるのは遅いが、最終的な性能もいまひとつである。
ドロップアウトの精度への効果
次に、\(p\) を変えてバリデーションセットに対する精度をプロットしてみる。
plt.clf()
plt.xlabel('epochs')
plt.ylabel('validation accuracy')
for i in range(0, len(hists)):
hist = hists[i]
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['val_acc'], label='$p={}$'.format(i * 0.1))
plt.legend()
plt.savefig('val_acc_dropout.png')
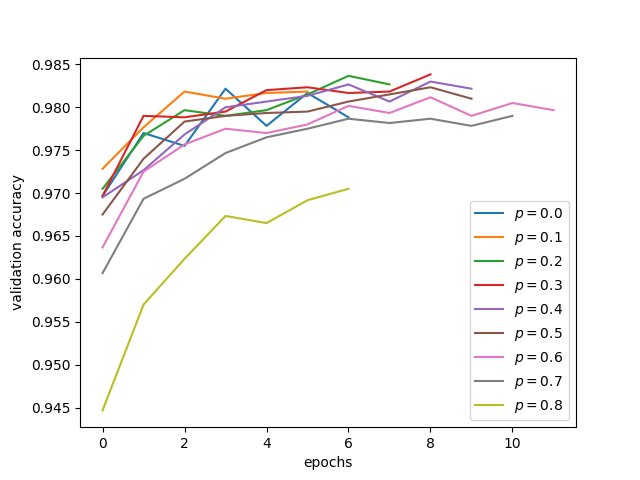
結局、正解率 98% 程度から最大で 0.3% 程度しか伸びていない。
学習結果の可視化
せっかく学習させたので、学習済のパラメータを使い、入力画像を実際に判定させてみる。
ドロップアウト確率としては、 さきほどの実験で最高スコアを達成した \(p = 0.3\) とする。
パラメータを利用するには、順方向の伝播を手動で計算してやれば良い。
def relu(x):
return np.maximum(x, 0, x)
# 入力層
u_1 = np.inner(X_test, weights[0].T) + weights[1]
z_1 = relu(u_1)
# 隠れ層
u_2 = np.inner(z_1, weights[2].T) + weights[3]
z_2 = relu(u_2)
# 出力層
u_3 = np.inner(z_2, weights[4].T) + weights[5]
z_3 = softmax(u_3)
y = z_3
# ラベル化
y_correct = np.argmax(y_test, 1)
y_predict = np.argmax(y, 1)
とりあえず、前回勉強したPrecision、Recallを計算してみる。
以下では、0から9までのPrecision、Recallを計算してプロットしてみた。
import Fscore as fscore
score = fscore.ThreatScore()
precisions = []
recalls = []
for i in range(0, 10):
score.calc(y_correct == i, y_predict == i)
precisions.append(fscore.precision(score))
recalls.append(fscore.recall(score))
plt.clf()
plt.xlabel('Number')
plt.plot(np.arange(0, 10), precisions, label='precision')
plt.plot(np.arange(0, 10), recalls, label='recall')
plt.legend()
plt.savefig('fscore.png')
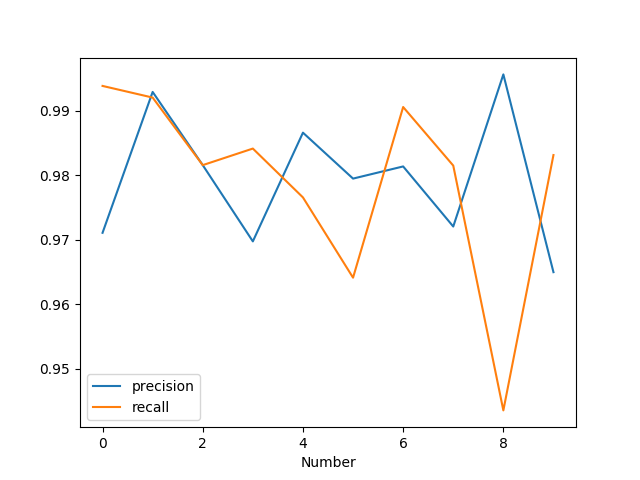
- 1はかなりの高確率で正解している。
- 8は誤爆しがち。
- Recall、Precisionがトレードオフになる様子が観察できる。
さらに、8について間違えたものを描いてみた。
y_correct_8 = y_correct == 8
y_predict_8 = y_predict == 8
X_failure = X_test[np.where(y_correct_8 != y_predict_8)]
y_failure = y_test[np.where(y_correct_8 != y_predict_8)]
y_predict_label = y_predict[np.where(y_correct_8 != y_predict_8)]
plt.clf()
for i in range(0, 32):
plt.subplot(4, 8, i+1)
pixels = X_failure[i]
pixels = pixels.reshape((28, 28))
plt.imshow(pixels, cmap='gray')
plt.title('{}'.format(y_predict_label[i]))
plt.savefig('failure8.png')
「これは当てて欲しかった」「これは正解がおかしいだろ」が混在する結果になった。

ソースコード
最後にソースコードを貼り付けておく。
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
from keras.callbacks import EarlyStopping
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(60000, 784) # 28 * 28
X_test = X_test.reshape(10000, 784)
X_train = X_train.astype('float32') / 255
X_test = X_test.astype('float32') / 255
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)
print('X_train.shape', X_train.shape)
print('X_test.shape', X_test.shape)
print('y_train.shape', y_train.shape)
print('y_test.shape', y_test.shape)
# ('X_train.shape', (60000, 784))
# ('X_test.shape', (10000, 784))
# ('y_train.shape', (60000, 10))
# ('y_test.shape', (10000, 10))
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dense(512, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
early_stopping = EarlyStopping(monitor='val_loss', patience=2)
hist = model.fit(X_train, y_train, batch_size=128, epochs=20,
validation_split=0.1, verbose=1, callbacks=[early_stopping])
score = model.evaluate(X_test, y_test, verbose=0)
print('score', score)
# ('score', [0.082287257276931036, 0.98250000000000004])
plt.clf()
plt.xlabel('epochs')
plt.ylabel('loss')
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['loss'], label='loss')
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['val_loss'], label='val_loss')
plt.legend()
plt.savefig('fit_loss.png')
hists = [ hist ]
for p in np.arange(0.1, 0.9, 0.1):
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(p))
model.add(Dense(512, activation='relu'))
model.add(Dropout(p))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
early_stopping = EarlyStopping(monitor='val_loss', patience=2)
hist = model.fit(X_train, y_train, batch_size=128, epochs=20,
validation_split=0.1, verbose=1, callbacks=[early_stopping])
hists.append(hist)
score = model.evaluate(X_test, y_test, verbose=0)
print('score', score)
plt.clf()
plt.xlabel('epochs')
plt.ylabel('loss')
for i in range(0, len(hists)):
hist = hists[i]
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['loss'], label='loss {}'.format(i * 0.1))
plt.legend()
plt.savefig('fit_loss_dropout.png')
plt.clf()
plt.xlabel('epochs')
plt.ylabel('validation loss')
for i in range(0, len(hists)):
hist = hists[i]
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['val_loss'], label='val_loss {}'.format(i * 0.1))
plt.legend()
plt.savefig('val_loss_dropout.png')
plt.clf()
plt.xlabel('epochs')
plt.ylabel('validation accuracy')
for i in range(0, len(hists)):
hist = hists[i]
plt.plot(np.arange(0, len(hist.history['loss'])),
hist.history['val_acc'], label='$p={}$'.format(i * 0.1))
plt.legend()
plt.savefig('val_acc_dropout.png')
p = 0.3
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dropout(p))
model.add(Dense(512, activation='relu'))
model.add(Dropout(p))
model.add(Dense(10, activation='softmax'))
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
early_stopping = EarlyStopping(monitor='val_loss', patience=2)
hist = model.fit(X_train, y_train, batch_size=128, epochs=20,
validation_split=0.1, verbose=1, callbacks=[early_stopping])
hists.append(hist)
score = model.evaluate(X_test, y_test, verbose=0)
print('score', score)
# ('score', [0.093335870010073263, 0.97950000000000004])
weights = model.get_weights()
print(map(lambda w:w.shape, weights))
# [(784, 512), (512,), (512, 512), (512,), (512, 10), (10,)]
def relu(x):
return np.maximum(x, 0, x)
def softmax(x):
max_x = np.max(x, 1)
exp_x = np.exp(x - max_x[:, None])
return exp_x / np.sum(exp_x, 1)[:, None]
# 入力層
u_1 = np.inner(X_test, weights[0].T) + weights[1]
z_1 = relu(u_1)
# 隠れ層
u_2 = np.inner(z_1, weights[2].T) + weights[3]
z_2 = relu(u_2)
# 出力層
u_3 = np.inner(z_2, weights[4].T) + weights[5]
z_3 = softmax(u_3)
y = z_3
y_correct = np.argmax(y_test, 1)
y_predict = np.argmax(y, 1)
import Fscore as fscore
score = fscore.ThreatScore()
score.calc(y_correct, y_predict)
precisions = []
recalls = []
for i in range(0, 10):
score.calc(y_correct == i, y_predict == i)
precisions.append(fscore.precision(score))
recalls.append(fscore.recall(score))
plt.clf()
plt.xlabel('Number')
plt.plot(np.arange(0, 10), precisions, label='precision')
plt.plot(np.arange(0, 10), recalls, label='recall')
plt.legend()
plt.savefig('fscore.png')
y_correct_8 = y_correct == 8
y_predict_8 = y_predict == 8
X_failure = X_test[np.where(y_correct_8 != y_predict_8)]
y_failure = y_test[np.where(y_correct_8 != y_predict_8)]
y_predict_label = y_predict[np.where(y_correct_8 != y_predict_8)]
plt.clf()
for i in range(0, 32):
plt.subplot(4, 8, i+1)
pixels = X_failure[i]
pixels = pixels.reshape((28, 28))
plt.imshow(pixels, cmap='gray')
plt.title('{}'.format(y_predict_label[i]))
plt.savefig('failure8.png')