CIFAR-10のPCA白色化/ZCA白色化
前回は Keras+CNNでCIFAR-10の画像分類 をしてみたが、 学習後のクラス判別精度が 71 % といまいちだった。
この精度を上げるため、データの前処理を勉強してみる。
1. 事前準備
本稿でもプログラムをいくつか書くが、前提として以下の通りライブラリのインポート、 およびデータのロードを済ませてある。
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
from keras.datasets import cifar10
from sklearn import preprocessing
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
print('x_train.shape', x_train.shape)
# ('x_train.shape', (50000, 32, 32, 3))
x_train = x_train.astype('float32') / 255
2. データの正規化
データの標準化ともいう。 データの偏りを小さくし、機械学習を進めやすくすることを目的に行う。
データサンプルの各成分について、平均 0 、分散 1 にそろえる変換処理を行う。
各サンプルを $ x_n $ とおくと、平均 $ \overline{x_n} $ は次のようにかける。
\[\overline{x_n} = \frac{1}{N} \sum_{n=1}^N x_{ni}\]ここで、 $ x_{ni} $ は $ x_n $ の各成分。
また、標準偏差は次のように定義する。
\[\sigma_i \equiv \sqrt{\frac{1}{N} \sum_{n=1}^N (x_{ni} - \overline{x_i})^2}\]平均 $ \overline{x_n} $ と標準偏差 $ \sigma_i $ を使い、標準化の変換は
\[x_{ni} \leftarrow \frac{x_{ni} - \overline{x_i}}{\sigma_i}\]を計算する。
では正規化をプログラムで実行し、可視化してみよう。
処理対象には CIFAR-10 の画像の7枚目を選んだ。特に意味は無い。
いったん7枚目の画像を描画。
plt.clf()
plt.imshow(x_train[6,:,:,:])
plt.savefig('cifar10_6.png')

図 2.1. CIFAR-10 データセットの6枚目の鳥
上記画像(を含む全データ)に対し正規化の変換を行う。
sklearn のライブラリを使った。全画像の各チャネルに対し正規化を実行。
x_train_std = np.zeros(x_train.shape)
for i in range(0, x_train.shape[0]):
for j in range(0, x_train.shape[3]):
x_train_std[i,:,:,j] = preprocessing.scale(x_train[i,:,:,j])
全ピクセルについて、横軸を赤、縦軸を青/緑としてプロットしてみた。 それほど意味は無い。なんとなく分布のようなものが見たかっただけ。
左が元データ、右が正規化後のデータである。
idx = 6
plt.clf()
plt.subplot(1, 2, 1)
plt.title('Before scaling')
plt.plot(x_train[idx,:,:,0].flatten(), x_train[idx,:,:,1].flatten(), 'gx')
plt.plot(x_train[idx,:,:,0].flatten(), x_train[idx,:,:,2].flatten(), 'bx')
plt.subplot(1, 2, 2)
plt.title('After scaling')
plt.plot(x_train_std[idx,:,:,0].flatten(),
x_train_std[idx,:,:,1].flatten(), 'gx')
plt.plot(x_train_std[idx,:,:,0].flatten(),
x_train_std[idx,:,:,2].flatten(), 'bx')
plt.savefig('cifar10_image_rgb.png')
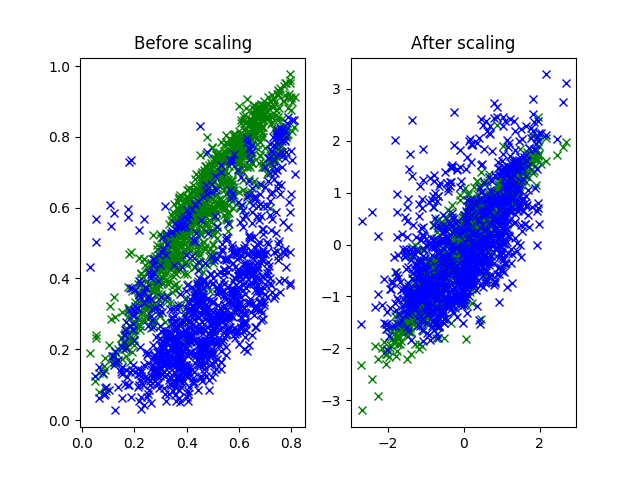
図 2.2. 正規化前後における緑、青成分の分布
左側では点の分布の中心と広がりが、緑と青ではずれていることが確認できる。
一方、右側では緑と青の点の分布の中心は $ (0, 0) $ になっている。 これはサンプルの緑、青成分の平均が 0 になったことを示す。
また、分布の広がる範囲についても大体同じくらいになった。 正規化により各成分の標準偏差が等しく 1 になったことを示す。
正規化前後の比較
正規化したデータをプロットしてみた。 正規化後のままだとプロットできる値になっていないので変換してから描く。
def normalizeMinMax(x, axis=0, epsilon=1E-5):
vmin = np.min(x, axis)
vmax = np.max(x, axis)
return (x - vmin) / (vmax - vmin + epsilon)
def normalizeImage(x):
img = x.reshape(x.shape[0] * x.shape[1], x.shape[2])
img = normalizeMinMax(img, axis=0)
return img.reshape(x.shape)
plt.clf()
for i in range(0, 16):
plt.subplot(4, 8, i*2+1)
fig = plt.imshow(x_train[i,:,:,:])
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.subplot(4, 8, i*2+2)
fig = plt.imshow(normalizeImage(x_train_std[i,:,:,:]))
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.savefig('cifar10_std.png')
出力は図2.3のようになった。各画像について、左側が正規化前、右側が正規化後。
人間的には画像が薄暗くなったような印象を受ける。
大体の傾向としては赤青緑や白など鮮やかな色が正規化により灰色っぽくなっている。 黒も灰色側に寄るようだ。これはさっき描いた色成分の分布を見ても当然のように思われる 。 ただし、左5, 6、上3の鹿の画像のような元々はっきりしないものは正規化により、 逆に特徴がよく見えるようになっている。元の画像は全体的に緑っぽかったが 正規化により緑が抑えられたことにより、他の赤青成分が相対的に目立つようになったため と思われる。

図 2.3. CIFAR-10画像の正規化前後比較
3. 白色化
白色化の目的も、訓練データの偏りを小さくして学習を進めやすくすることである。
ただし白色化では正規化よりも凝った変換を行い、訓練データの各成分間の相関も無くしてしまう。なぜ相関を無くすかというと、データの成分間に相関があるとその分だけデータを近似するモデルが複雑になるということだろう。なんとなくわかる気がする。
正規化の項で描いたプロット(図 2.2)を見ると、緑も青も右肩上りの分布になっている。 これは横軸にした赤成分と、縦軸にした緑、青成分に相関があることを表す。
白色化では訓練データに対しデータの各成分間の相関を無くすような線形変換を行う。 この変換を行う変換は無数にあるのだが、その変換の選び方により PCA 白色化とか ZCA 白色化とかいう。
$ D $ 次元空間の生の訓練データサンプルを $ \boldsymbol{x} = [ x_1, x_2, …, x_D ] $ とおく。
このデータは大体の場合平均が 0 でない。 このままでは白色化について考える上で邪魔なので、変換して各成分の平均を 0 にした N 個のデータサンプルをそれぞれ $ \boldsymbol{x}_1, \boldsymbol{x}_2, …, \boldsymbol{x}_N $ とおく。
各成分の平均が 0 であることは
\[\frac{1}{N} \sum^N_{n=1} \boldsymbol{x}_n = \boldsymbol{0}\]と表現する。パッと見、スカラの計算のようだが右側は全ての要素が 0 の行列である。
分散共分散行列というのは各サンプル間の相関を行列で一気に表したものである。 例えば 3 次元空間の場合、共分散行列は次のようにかける。
\[\Phi_X = \begin{bmatrix} \sigma_1^2 & \sigma_{12} & \sigma_{13} \\ \sigma_{21} & \sigma_2^2 & \sigma_{23} \\ \sigma_{31} & \sigma_{32} & \sigma_3^2 \end{bmatrix}\]ここで $ \sigma_{12} $ というのは1次元と2次元の成分間の相関、 すなわち $ x_1 $ と $ x_2 $ がどれだけ同じように変化するかを現わしている。 2成分の相関が無い状態というのは、それらが一切連動していないことであり $ \sigma_{12} = 0 $ になる。
任意の各成分間の相関が無いとき、$ \Phi $ の非対角成分 $ \sigma_{12} $ や $ \sigma_{13} $ などが全て 0 であり、すなわち $ \Phi $ は対角行列である。
$ \boldsymbol{x} $ の分散共分散行列は以下のようにして計算できる。
\[\Phi_\boldsymbol{x} = \frac{1}{N} \sum_{n=1}^{N} \boldsymbol{x}_n \boldsymbol{x}_n^{\mathrm{T}} = \frac{1}{N} X X^{\mathrm{T}}\]ここで各成分間の相関を無くした共分散行列を $ \Phi_U $ とすると、
\(\Phi_U = \frac{1}{N} \sum_{n=1}^{N} u_n u_n^{\mathrm{T}} = \frac{1}{N} U U^{\mathrm{T}}\) 。
ただし、相関を無くす線形変換を $ P $、変換後のデータを $ u_n $ とし、
\[u_n = P \boldsymbol{x}_n \quad (n=1, ..., N)\]と表す。
変換後のデータに各成分間の相関が無いとき、 $ \Phi_U $ は非対角成分の値が全て 0 、つまり対角行列である。 対角行列ならばなんでもいいので $ \Phi_U = I $ としてしまう。
すると、
\[\frac{1}{N} \ U \ U^{\mathrm{T}} = \Phi_U = I\]とかけるので、これに $ U = PX $ を代入し、
\[\begin{eqnarray} \frac{1}{N} \ (PX) \ (PX)^{\mathrm{T}} &=& I \\ \frac{1}{N} \ P \ X \ X^{\mathrm{T}} \ P^{\mathrm{T}} &=& I \\ \frac{1}{N} \ P \ (N \ \Phi_\boldsymbol{x}) \ P^{\mathrm{T}} &=& I \\ P \ \Phi_\boldsymbol{x} \ P^{\mathrm{T}} &=& I \\ \Phi_\boldsymbol{x}^{-1} &=& P^{\mathrm{T}} \ P \end{eqnarray}\]式変形には転置行列の性質 $ (AB)^{\mathrm{T}} = B^{\mathrm{T}} \ A^{\mathrm{T}} $ および 逆行列の性質 $ (AB)^{-1} = B^{-1} A^{-1} $ を使った。
ここで $ \Phi_X $ の固有ベクトルを縦に並べた行列を $ E $、 $ \Phi_X $ の固有値を対角に並べた行列を $ D $ とおくと、 固有ベクトルの定義より、
\[E^{-1} \ \Phi_X \ E = D\]とかくことができる。
ただし $ \Phi_X $ は対称行列としていたので $ E $ は直行行列、すなわち $ E^{-1} = E^{\mathrm{T}} $ が成り立つ。
これらより、
\[\begin{eqnarray} E^{-1} \ \Phi_X \ E &=& D \\ \Phi_X &=& E \ D \ E^{-1} \\ \Phi_X^{-1} &=& (E \ D \ E^{-1})^{-1} \\ \Phi_X^{-1} &=& E \ D^{-1} \ E^{-1} \\ \Phi_X^{-1} &=& E \ D^{-1} \ E^{\mathrm{T}} \\ \end{eqnarray}\]さらに、$ \Phi_X^{-1} = P^{\mathrm{T}} \ P $ だったので、
\[\begin{eqnarray} P^{\mathrm{T}} \ P &=& E \ D^{-1} \ E^{\mathrm{T}} \\ P &=& Q \ D^{-1/2} \ E^{\mathrm{T}} \\ \end{eqnarray}\]ここで $ D^{-1/2} $ は対角行列 $ D $ の各要素を $ -1/2 $ 乗した行列、 $ Q $ は $ P $ と同じサイズの直行行列である。
PCA 白色化
正直さっきの最後の変形と $ Q $ が出てくるところはよくわかっていないが、 $ Q $ は $ P $ と同じサイズの直行行列ならばよいということで、$ Q = I $ でもよい。
このときの変換 $ P $ を PCA 白色化 (PCA Whitening) と呼ぶ。 固有ベクトル $ E $ を利用しており、PCA 分析 (PCA=Principal component analysys; 主成分分析) と似ているところかららしい。
\[P = D^{-1/2} \ E^{\mathrm{T}}\]PCA 分析についてはまた今度ということにする。
PCAの実装は次のようになった。
class PCAWhitening:
def __init__(self, epsilon=1E-6):
self.epsilon = epsilon
self.mean = None
self.eigenvalue = None
self.eigenvector = None
self.pca = None
def fit(self, x):
self.mean = np.mean(x, axis=0)
x_ = x - self.mean
cov = np.dot(x_.T, x_) / x_.shape[0]
E, D, _ = np.linalg.svd(cov)
D = np.sqrt(D) + self.epsilon
self.eigenvalue = D
self.eigenvector = E
self.pca = np.dot(np.diag(1. / D), E.T)
return self
def transform(self, x):
x_ = x - self.mean
return np.dot(x_, self.pca.T)
固有値、固有ベクトルの計算にはSVDのライブラリを使った。 参考サイトのまねである。
SVD(Singular value decomposition)は特異値分解といい、 行列の対角化を行うところや、次元数削減のために利用する点がPCA分析と似ている。
ともかく、上記の $ E $、$ D $ を求める計算では対角化を行うため、 SVDのライブラリが割とそのまま使える模様。
作った PCAWhitening を以下のようにして使う。
少し悩んだが、一枚の画像の全ピクセルのRGBを1列の展開し、 特徴量として渡してやるのが正解のようだ。
def normalizeImage2(x, epsilon=1E-6):
vmin = np.min(x)
vmax = np.max(x)
return (x - vmin) / (vmax - vmin + epsilon)
x_pcaw = x_train.reshape(x_train.shape[0], -1)
print('x_pcaw.shape=' + str(x_pcaw.shape))
# x_pcaw.shape(50000, 3072)
pcaw = PCAWhitening().fit(x_pcaw)
x_pcaw = pcaw.transform(x_pcaw).reshape(x_train.shape)
plt.clf()
for i in range(0, 16):
plt.subplot(4, 8, i*2+1)
fig = plt.imshow(x_train[i,:,:,:])
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.subplot(4, 8, i*2+2)
fig = plt.imshow(normalizeImage2(x_pcaw[i,:,:,:]))
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.savefig('cifar10_pcaw.png')
出力は図3.1のようになった。 左右に隣接する画像が2枚ずつペアで、左側が元画像、右側がPCA白色化した結果。
もはやなんだかわからないが、PCA白色化というのはそういうものらしい。 左上が低周波成分、右下が高周波成分と考えていいのだろうか?
本によると「自然画像は一般に低い周波数成分ほど値が大きい特徴があり、PCA白色化はこれをキャンセルする」とのこと。
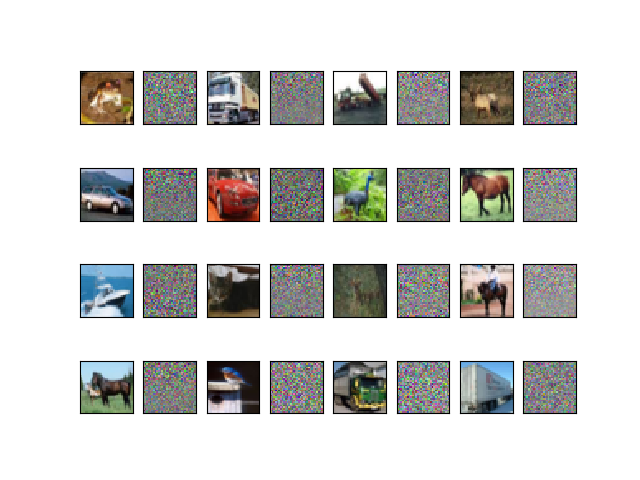
図 3.1. CIFAR-10画像のPCA白色化
フィルタをプロットしてみる。
plt.clf()
for i in range(0, 96):
plt.subplot(8, 12, i+1)
fig = plt.imshow(normalizeImage2(img[i,:]).reshape(32, 32, 3))
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.savefig('cifar10-pca-filter.png')
plt.clf()
for i in range(0, 96):
plt.subplot(8, 12, i+1)
fig = plt.imshow(normalizeImage2(img[i*32,:]).reshape(32, 32, 3))
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.savefig('cifar10-pca-filter-2.png')
低周波成分を強調するフィルタから始まり、段々と高周波に移っていく3,072枚のフィルタが得られた。

図3.2a. CIFAR-10画像のPCA白色化フィルタ 1-96枚目

図3.2b. CIFAR-10画像のPCA白色化フィルタ 1-3072枚目まで32枚飛ばし
あと、少しPCA分析(主成分分析)もしてみる。
PCA白色化の処理の途中で、固有ベクトル、固有値が計算されている。 固有値は大きい順に並んでいて、対応する固有ベクトルの寄与率がわかる。
せっかくだから寄与率を計算してみる。
explained_variance_ratio = pcaw.eigenvalue / np.sum(pcaw.eigenvalue)
explained_variance = np.cumsum(explained_variance_ratio)
plt.clf()
plt.plot(np.arange(1, explained_variance.shape[0]+1, 1.0), explained_variance)
plt.savefig('cifar10-pca-explained_variance.png')
print('explained_variance[1536]=' + str(explained_variance[1536]))
# explained_variance[1536]=0.94648
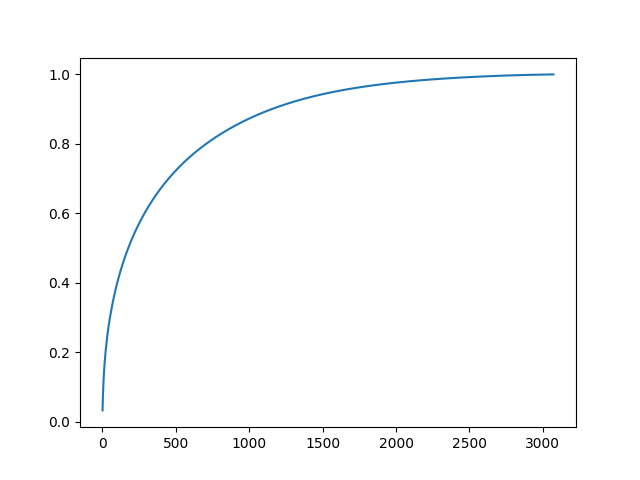
図 3.3. CIFAR-10画像のPCA分析 主成分の寄与率
全体の半分のデータ数があれば、データの特徴を95%くらい抑えられるようだ。
ZCA 白色化
先程の式は、
\[Q^{-1} \ P \ E = D^{-1/2}\]に変形できる。 ここで $ Q = E $ とすると、$ P $ は対称行列に制限される。
このときの $ P $ は ZCA 白色化 (ZCA=Zero-phase component analysis; ゼロ位相成分分析)と呼ぶ。
\[P = E \ D^{-1/2} \ E^{\mathrm{T}}\]ZCAの実装はほぼPCAと同じで、以下のようになった。
class ZCAWhitening:
def __init__(self, epsilon=1E-6):
self.epsilon = epsilon
self.mean = None
self.zca = None
def fit(self, x):
self.mean = np.mean(x, axis=0)
x_ = x - self.mean
cov = np.dot(x_.T, x_) / x_.shape[0]
E, D, _ = np.linalg.svd(cov)
D = np.sqrt(D) + self.epsilon
self.zca = np.dot(E, np.dot(np.diag(1.0 / D), E.T))
return self
def transform(self, x):
x_ = x - self.mean
return np.dot(x_, self.zca.T)
使ってみる。
x_zcaw = x_train.reshape(x_train.shape[0], -1)
zcaw = ZCAWhitening().fit(x_zcaw)
x_zcaw = zcaw.transform(x_zcaw).reshape(x_train.shape)
plt.clf()
for i in range(0, 16):
plt.subplot(4, 8, i*2+1)
fig = plt.imshow(x_train[i,:,:,:])
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.subplot(4, 8, i*2+2)
fig = plt.imshow(normalizeImage(x_zcaw[i,:,:,:]))
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.savefig('cifar10_zcaw.png')
出力は図3.4のようになった。 PCA白色化と違い、これは何が起きているのか見て理解できそうだ。輪郭が強調されている。

図 3.4. CIFAR-10画像のZCA白色化
ZCA白色の変換を可視化してみると、 各ピクセル、各色成分について隣との差分を強調するフィルタになっている様子が見られるらしい。
print('zcaw.zca.shape=' + str(zcaw.zca.shape))
# zcaw.zca.shape=(3072, 3072)
img = zcaw.zca
vmin = np.min(img, axis=0)
vmax = np.max(img, axis=0)
img = (img - vmin) / (vmax - vmin)
plt.clf()
for i in range(0, 24):
plt.subplot(4, 6, i+1)
fig = plt.imshow(img[i,:].reshape(32, 32, 3)[0:8,0:8,0:3])
fig.axes.get_xaxis().set_visible(False)
fig.axes.get_yaxis().set_visible(False)
plt.savefig('cifar10-zca-filter.png')
図 3.5がそれである。 フィルタ3枚ずつが組になり、同じ位置に赤、緑、青の目が現れている。 次の3枚では隣のピクセルに目が現われていて、やはり赤、緑、青の組合せである。
また、目に隣接するピクセルは目の色の補色になっている。 これが各ピクセル、各色成分について隣との差分を強調するフィルタの正体のようだ。

図 3.5. CIFAR-10画像のZCA白色化フィルタ
なお、フィルタを見易くするために、左上8x8だけをプロットした。
計算時のテクニック
上記のプログラムには実装済みだが、 $ D $ には値がとても小さい成分が入っていると、 $ D^{-1/2} $ の値が極端に大きくなってしまい計算時に問題になるとのこと。
この対策として、小さい値 $ \varepsilon $ (例: $ 10^{-6} $) だけ加算してあげてから計算に使えばよい。
\[\begin{eqnarray} P_{PCA} &=& (D^{\frac{1}{2}} + \varepsilon I)^{-1} \ E^{\mathrm{T}} \\ P_{ZCA} &=& E \ (D^{\frac{1}{2}} + \varepsilon I)^{-1} \ E^{\mathrm{T}} \end{eqnarray}\]RGB分布
PCA白色化、ZCA白色化をかけた画像についても、横軸を赤、縦軸を青/緑として全ピクセル分プロットしてみた。
idx = 6
def plot_rgb(x):
vmax = np.max(np.abs(x[idx,:,:,:]))
plt.plot(x[idx,:,:,0].flatten(), x[idx,:,:,1].flatten(), 'gx')
plt.plot(x[idx,:,:,0].flatten(), x[idx,:,:,2].flatten(), 'bx')
plt.xlim(-vmax, vmax)
plt.ylim(-vmax, vmax)
plt.clf()
plt.subplot(2, 2, 1)
plt.title('Before scaling')
plt.plot(x_train[idx,:,:,0].flatten(), x_train[idx,:,:,1].flatten(), 'gx')
plt.plot(x_train[idx,:,:,0].flatten(), x_train[idx,:,:,2].flatten(), 'bx')
plt.subplot(2, 2, 2)
plt.title('After scaling')
plot_rgb(x_train_std)
plt.subplot(2, 2, 3)
plt.title('PCA Whitening')
plot_rgb(x_pcaw)
plt.subplot(2, 2, 4)
plt.title('ZCA Whitening')
plot_rgb(x_zcaw)
plt.savefig('cifar10_image_rgb2.png')
出力は図3.6。 正規化(右上)では斜め方向に伸びていることからRGBの相関があることが確認できたが、 PCA白色化(左下)、ZCA白色化(右下)ではそれが見られなくなっている。 白色化によって成分間の相関を除去できたといえそうだ。
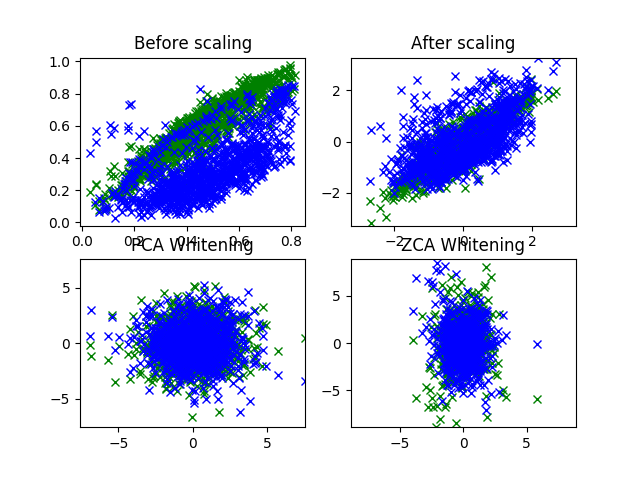
図 3.6. CIFAR-10 鳥画像のRGB分布比較
参考
白色化
- 岡谷貴之, 「深層学習」第5章, 講談社, 2016.
- 深層学習オートエンコーダー
- データの前処理〜白色化 その1〜 - KDOG Notebook
- CIFAR-10 と ZCA whitening - まんぼう日記
- データの前処理〜白色化 その2〜 - KDOG Notebook
- zca/zca.py at master - mwv/zca